對這個問題實在太有緣了,這是我上課唯一有認真聽的一段
考試剛好考出來,所以為了紀念它
我整理一下,寫在這邊……~”~
要解這個問題要知道三件事情
1.需要多少步驟
2.在那個步驟移動那個盤子
3.要把這個盤子移到那個柱子
為了要方便了解這些規則,先放張我自己畫的圖,有點醜,但我很努力了~”~
這個是以盤子總數為4的例子
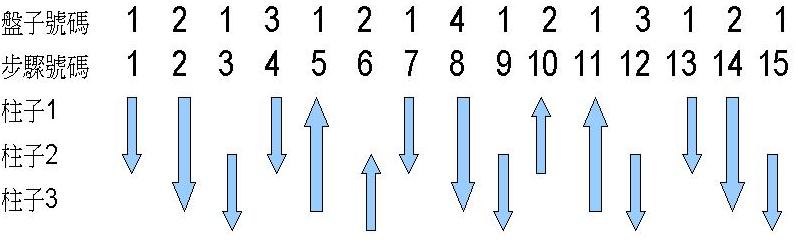
移動步驟的總數應該不難,大家很常聽到的,就是2^n-1,n表示要移動的盤子數
接著要找那個盤子,最簡單的一看就知道,只要是奇數步驟的,都會移動1號盤子
其他的步驟以k表示,看k能除以幾次2,再加1就是要移動的盤子號碼,但若商數是奇數則停止….
說簡單一點,就是能被2整除幾次,再加1
例如步驟14,14/2=7,無法再整除,所以是1+1=2,要移動盤子2號
若是步驟12,12/2=6,可以再整除,6/2=3,不能整除了,所以除了2次再加1,所以要移動盤子3號
以此類推….
然後就是很難稿的移動到那個柱子
如果盤子總數是奇數,則盤子號碼為奇數的盤子以逆時針方向旋轉、盤子號碼為偶數的盤子以順時針方向旋轉
如果盤子總數是偶數,則盤子號碼為奇數的盤子以順時針方向旋轉、盤子號碼為奇數的盤子以逆時針方向旋轉
做個簡單的表格好了~”~
| 奇數號碼盤子 | 偶數號碼盤子 | |
| 總數偶數 | 順時針 | 逆時針 |
| 總數奇數 | 逆時針 | 順時針 |
恩…就差不多這樣,依照這些規則
就有辦法寫出非遞迴的河內塔程式了~